蛮力法解决最近对问题（可视化）

题目

1、实验目的
通过本实验，掌握蛮力法解决问题的算法效率分析方法，运用蛮力法解决问题的思想，解决实际问题。
2、实验内容
运用蛮力法的基本思想解决凸包问题、最近对问题。打印输出。
3、实验要求
（1）运用面向对象程序设计语言来做；
（2）实现可视化的效果；
（3）输入规模不得少于20。

算法概述

创建点的对象的类，随着接收用户的键盘输入（x,y），将类实例化为一个个对象，并用对象数组盛放
（注意new和 delete的方法），接着初始化一个结果数组result（置于全局）,选一个足够大的数最为初始的
距离（确保此距离一定会更新，同时给其赋值也保证了判断的一致性），点的x,y值取-1（真实的点中不存在
对应默认的对象创建函数将x和y赋值为-1(表示数组此位置的对象不是点)，保持一致性),然后用打擂台的方法
如果(x1-x2)^2+(y1-y2)^2的值比result[2]的小，就更新result的三个值，更新到最后就得到了结果；为了
可视化，在更新遍历的过程中，将map（地图）对应位置的零置1，表示此处存在点；最后的最近对的点map
对应位置置2，就区别开来，打印map时，根据map对应位置的值打印出不同的图形，即可视化了

遍历方法优化（所有点握一次手就行）

C++代码实现

#include <iostream>
#include<math.h>

using namespace std;

class Point
{
public:
	Point() { x = -1; y = -1; show_or_not = false; }
	Point(int xx, int yy) { x = xx; y = yy; show_or_not = true; }
	bool show()
	{
		return show_or_not;
	}
	int show_x()
	{
		return x;
	}
	int show_y()
	{
		return y;
	}
private:
	int x;
	int y;
	bool show_or_not;
};
int map[10][10] = { 0 }; //可视化地图
int result[3]; //结果点集对象的下标和最小距离的平方作为结果  
int main()
{
	int a, b;
	int i = 0;
	Point *p = new Point[100];
	cout << "请输入点对（小于10的非负整数，两个一行，回车输入下一个，输入-1 -1结束输入）" << endl;
	cin >> a >> b;
	while (!(a == -1 && b == -1))
	{
		p[i] = Point(a, b);
		i++;
		cin >> a >> b;
	}
	i = 0;
	while (p[i].show())
	{
		map[p[i].show_x()][p[i].show_y()] = 1;
		i++;
	}
	int min_dis = 50000; //定义一个足够大的数初始化最小值
	for (int j = 0; j < i; j++) //找出最近对
	{
		for (int t = j + 1; t < i; t++)
		{
			int xx = (p[j].show_x() - p[t].show_x());
			int yy = (p[j].show_y() - p[t].show_y());
			if ((xx*xx + yy * yy) < min_dis)
			{
				min_dis = xx * xx + yy * yy;
				result[0] = j;
				result[1] = t;
				result[2] = min_dis;
			}
		}
	}
	cout << "最近点对是：" << "[" << p[result[0]].show_x() << "," << p[result[0]].show_y() << "]";
	cout << "[" << p[result[1]].show_x() << "," << p[result[1]].show_y() << "]" << endl;
	cout << "最近距离是:" << pow((result[2]), 0.5) << endl;

	//画地图
	map[p[result[0]].show_x()][p[result[0]].show_y()] = 2;
	map[p[result[1]].show_x()][p[result[1]].show_y()] = 2;
	cout << endl;
	for (i = 0; i < 10; i++)
	{
		for (int j = 0; j < 10; j++)
		{
			if (map[i][j] == 0)
				printf("一");
			else if (map[i][j] == 1)
				printf("点");
			else
				printf("对");
		}
		cout << endl;
	}
	delete []p; //清除堆区对象数组
	return 0;
}

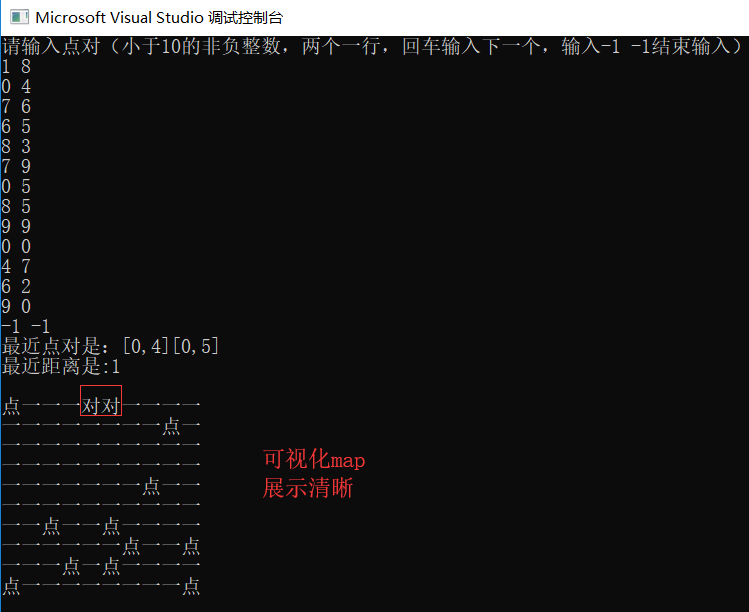
运行效果图