活动安排-贪心算法-可视化

前情提要

有n个活动(假设n很大，人力安排较困难)

n个活动的开始时间和结束时间已经知道

但我又想充分利用资源，安排最多数量的活动

贪心算法

语言：python

可视化依赖的第三方库：numpy,matplotlib

开始活动安排之旅

贪心算法概述：

    创建活动类（或结构体）,按照用户输入实例化为一个个活动对象,按照活动的结束时间增序对活
动整体排序，挑选活动时，活动的结束最早的优先被选取，为剩下活动留下最多的时间来安排（每次使剩下的时间可能安排最多的活动，或说是每次自己占用的时间资源最少），是谓贪心。

细节

    算法的实现不依赖于具体的语言，但为了可视化的便捷，我未能阻挡python的有货
    放数据的容器选择了Python的苦力：列表。按照对象的属性值排序用了sort函数，只有一行，
突出贪心算法
    实现过程：一个已经按结束时间排好序的对象列表，第一个活动定被选入，看第二个活动是否
与最后一个被选入的活动冲突（只看其开始时间即可），冲突否？不选:选;然后看下一个，重复判断冲突的过程……，即欧克
    为了可视化，将对象加个属性（标记）：select;初始化为false
    可视化的部分照葫芦画个瓢,下给小demo,有接口API,传入数据就ok

上代码(python3)

import matplotlib.pyplot as plt

class Activation(object):
    def __init__(self,start,end,id):
        self.start = start
        self.end = end
        self.select = False
        self.id = id

def main():
    act_num = eval(input("请输入活动总的个数："))
    act_list = []
    for i in range(act_num):
        a = eval(input("请输入第{}个活动起始时间：".format(i+1)))
        b = eval(input("请输入第{}个活动结束时间：".format(i+1)))
        if a>=b:
            print("error:结束时间小于等于了开始")
            b = eval(input("请重新输入第{}个活动结束时间：".format(i+1)))
        act_list.append(Activation(a,b,i+1))
    act_list.sort(key = lambda obj:obj.end,reverse = False)
    last = 0
    for i in range(act_num):
        if i==0:
            act_list[i].select = True
        elif act_list[i].start >= act_list[last].end:
            act_list[i].select = True
            last = i
    #可视化（结果）
    fig, ax = plt.subplots()
    order = 1  #行数
    for i in act_list:
        if i.select == True:
            ax.broken_barh([(i.start,i.end-i.start)], (10*order,9),facecolor='green')
        else:
            ax.broken_barh([(i.start,i.end-i.start)], (10*order,9),facecolor='blue')
        order = order + 1
    ax.set_ylim(5, 10*act_num+15)
    #自适应大小
    ax.set_xlim(0, act_list[-1].end)
    ax.set_xlabel('time order')
    act_y = []
    act_lebal = []
    for i in range(act_num):
        act_y.append(10*i+15)
        act_lebal.append("activity{}".format(act_list[i].id))
    ax.set_yticks(act_y)
    ax.set_yticklabels(act_lebal)
    ax.grid(True)
    ax.annotate('race interrupted', (61, 25),
                xytext=(0.8, 0.9), textcoords='axes fraction',
                arrowprops=dict(facecolor='black', shrink=0.05),
                fontsize=16,
                horizontalalignment='right', verticalalignment='top')

    plt.show()

main()

运行效果：

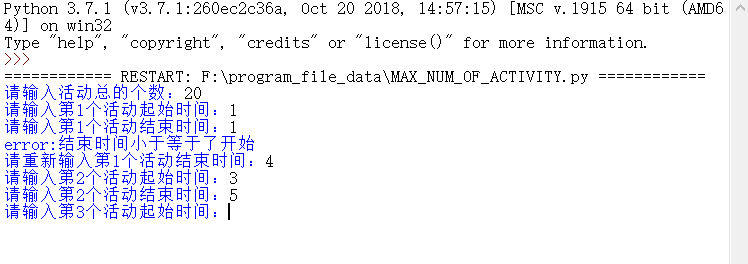
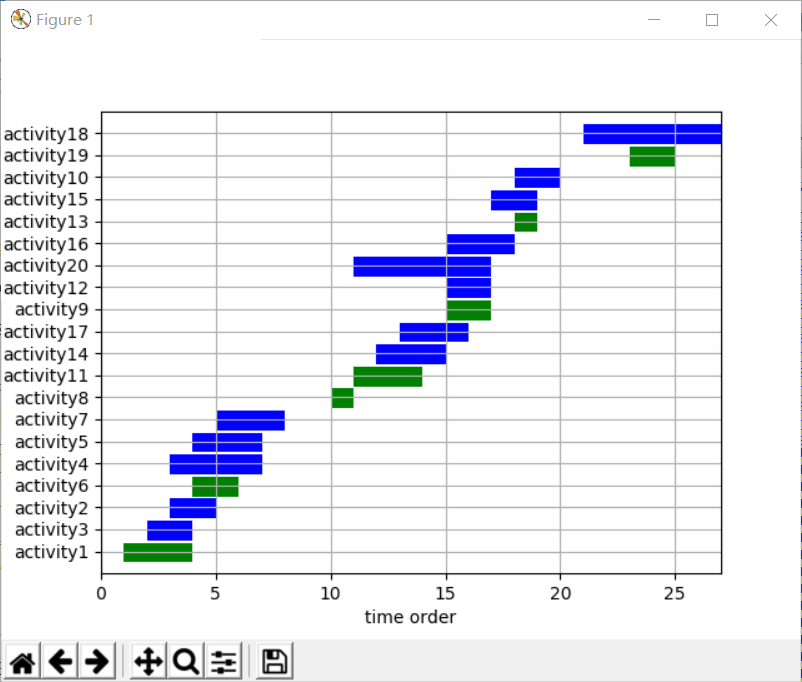
matplotlib的一个小demo

import matplotlib.pyplot as plt

fig, ax = plt.subplots()
ax.broken_barh([(110, 30), (150, 10)], (10, 9), facecolors='blue')
ax.broken_barh([(10, 50), (100, 20), (130, 10)], (20, 9),
               facecolors=('red', 'yellow', 'green'))
ax.set_ylim(5, 35)
ax.set_xlim(0, 200)
ax.set_xlabel('seconds since start')
ax.set_yticks([15, 25])
ax.set_yticklabels(['Bill', 'Jim'])
ax.grid(True)
ax.annotate('race interrupted', (61, 25),
            xytext=(0.8, 0.9), textcoords='axes fraction',
            arrowprops=dict(facecolor='black', shrink=0.05),
            fontsize=16,
            horizontalalignment='right', verticalalignment='top')

plt.show()

小demo样式

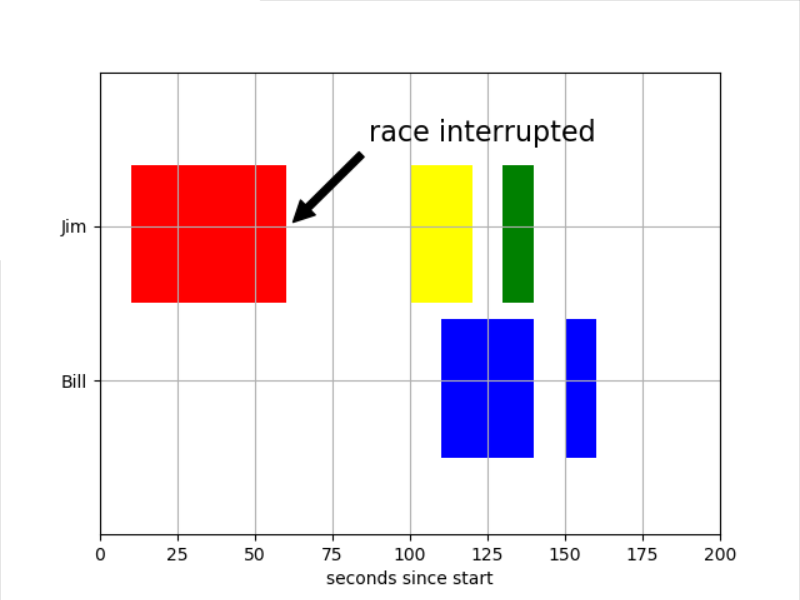
还是有所顾虑，因为局部的最优解不一定累积为全局最优解

给出证明：

暂未想出清晰证明方法，希望群策群力，帮忙相出一个好的证明方法，请评论，

评论未开可在github提出issue,感谢