探寻宝藏_动态规划和路径遍历

问题描述

传说HMH大沙漠中有一个M*N迷宫，里面藏有许多宝物。某天，Dr.Kong找到了迷宫的地图，他发现迷宫内处处有宝物，最珍贵的宝物就藏在右下角，迷宫的进出口在左上角。当然，迷宫中的通路不是平坦的，到处都是陷阱。Dr.Kong决定让他的机器人卡多去探险。

但机器人卡多从左上角走到右下角时，只会向下走或者向右走。从右下角往回走到左上角时，只会向上走或者向左走，而且卡多不走回头路。（即：一个点最多经过一次）。当然卡多顺手也拿走沿路的每个宝物。

Dr.Kong希望他的机器人卡多尽量多地带出宝物。请你编写程序，帮助Dr.Kong计算一下，卡多最多能带出多少宝物。

输入

第一行： K 表示有多少组测试数据。
接下来对每组测试数据：
第1行: M N
第2~M+1行： Ai1 Ai2 ……AiN (i=1,…..,m)
【约束条件】
2≤k≤5 1≤M, N≤50 0≤Aij≤100 (i=1,….,M; j=1,…,N)
所有数据都是整数。 数据之间有一个空格。
输出
对于每组测试数据，输出一行：机器人卡多携带出最多价值的宝物数

样例输入

2
2 3
0 10 10
10 10 80
3 3
0 3 9
2 8 5
5 7 100

样例输出

120
134

问题简单描述


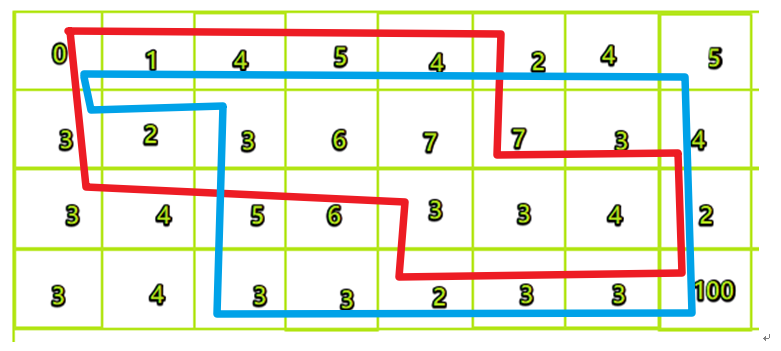
如图简单所示，在类似红蓝标记的这样（过左上角（起点）和右下角（最深处）并且无交叉）的所有可能的回路中找到一条能使路过的位置的权值（宝藏价值）之和最大的回路并能输出其权值之和，这个问题就算解决了
由于卡多走路的方式所限：回路的任意一单位段的连接必须满足只有上下相邻或左右相邻的点间可连接的条件

解决方法

动态规划法

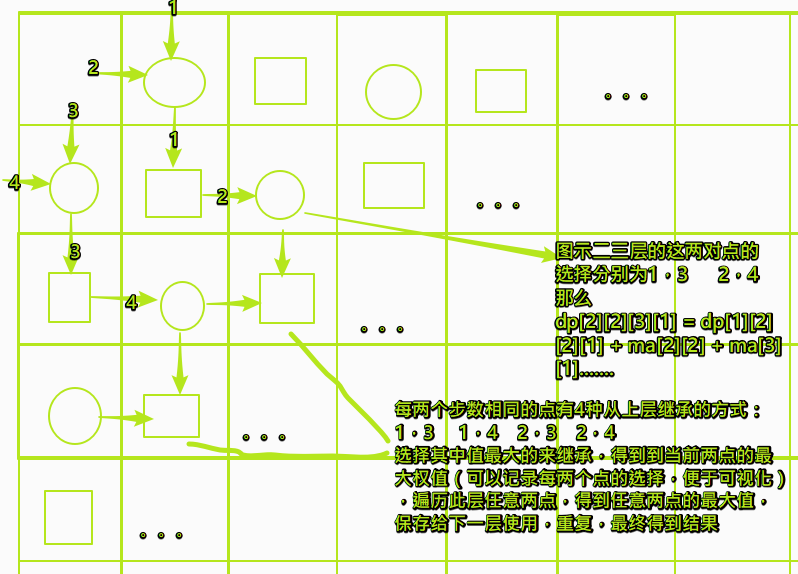
这是双进程DP问题，首先，假设出发点为A 终点为B 那么，根据题目给出的条件，可以推出A->B的动态转移方程
为 dp[i][j] = max(dp[i-1][j],dp[i][j-1]) + a[i][j]; 由于，同理可得B的情况，那么，题目的意思是A->B
然后 B -> A我们可以假设同时从A点出发，得到两条不同路径，这个是一样的效果。所以，我们可以得到一个动
态转移方程
dp[i][j][p][q] = max(dp[i-1][j][p-1][q],dp[i-1][j][p][q-1],dp[i][j-1][p-1][q],dp[i][j-1][p][q-1])+
ma[i][j] + ma[p][q]
因为 每次只能移动一步，即 i+1 或j+1 那么 i+j是移动的步数 因为从A点开始移动的，经过相同的步数，肯
定能得到i+j = p+q，还有一点要注意一下，这题与NYOJ 61是同类问题，但是，有一点细节要注意，最后终点的
值也要算上，上面的动态方程得到的值不包含两个A 和 B的值，因为A是起点，所以，他的值一般是0，所以，得
到最后的结果应该是
sum = max(dp[m-1][n][m-1][n],dp[m-1][n][m][n-1],dp[m][n-1][m-1][n],dp[m][n-1][m][n-1]) + ma[m][n]

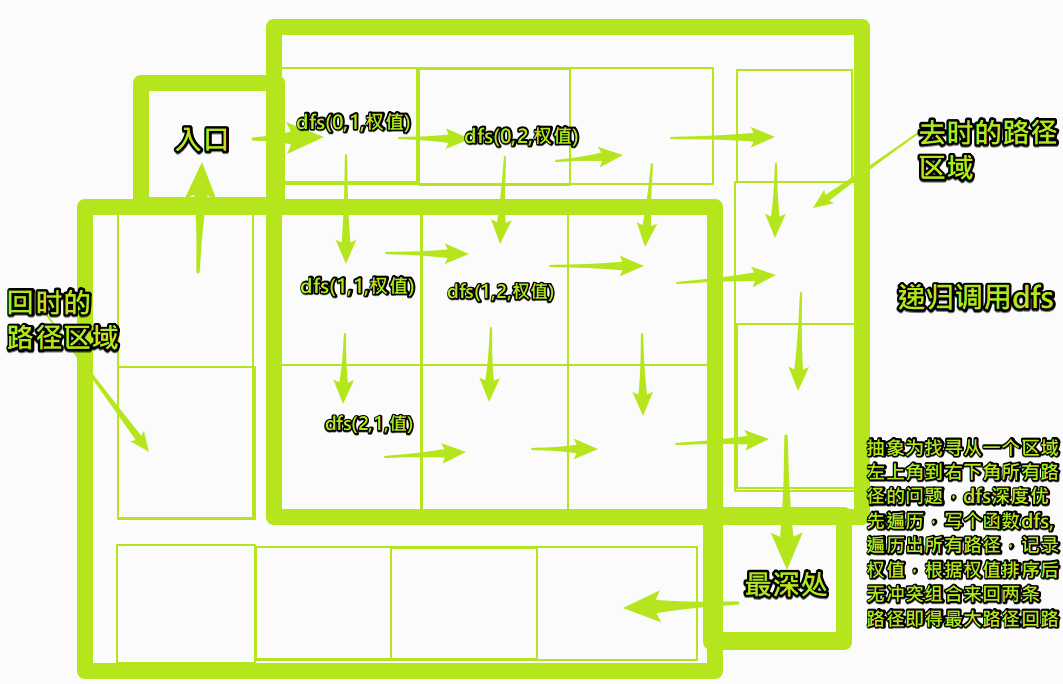
DFS(深度优先搜索：针对路径而非结点)

深度优先搜索（根据卡多走路的规则，即只能向下或向右走可确定结点间的可达关系），这样可以轻松地将从入口到右下角所有的路径遍历出来，定义路径对象的类，保存每一条路径，因为卡多的路径是来回两个的，所以两类对象两两组合，根据组合的路径的宝物总价值对组合进行排序，选出宝物总价值最大且路径不冲突的组合作为结果即可。

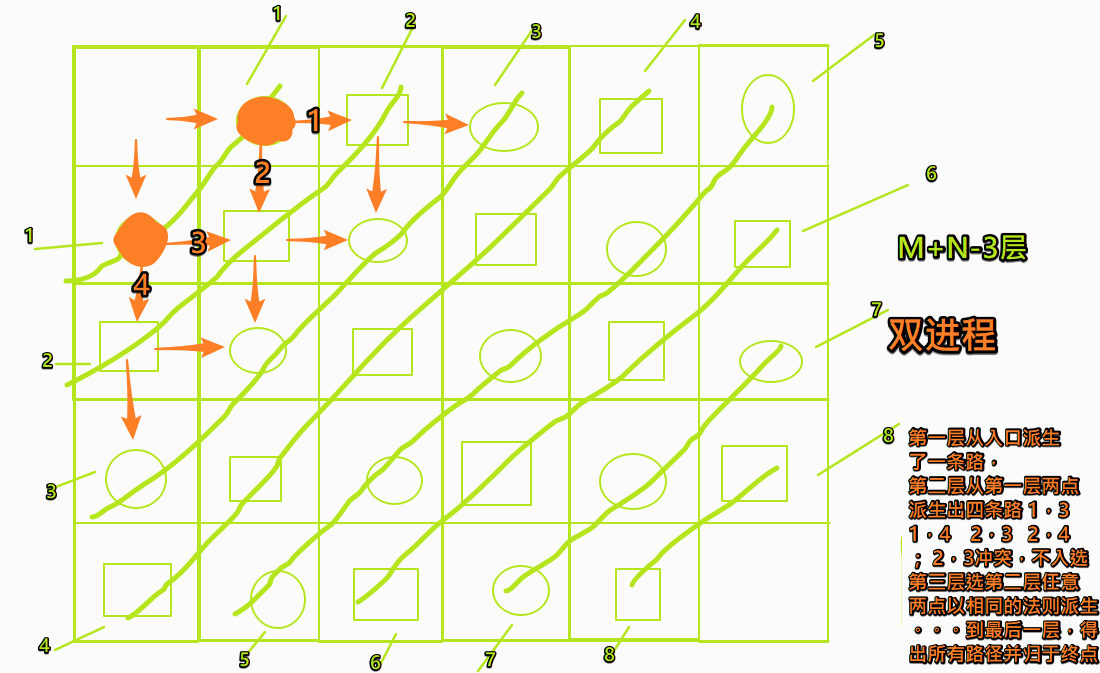
BFS(广度优先搜索：针对路径而非结点)

广度优先搜索（类似动态规划的过程，双进程进行，从入口同时出发不相交的两条路径作为卡多的来回两条路径，广度优先的方便之处是可以在相同步数的层次内继承上一层次的结果根据卡多走路的规则和不相交的约束可以快速确定走到此层次的所有路径）出所有的路径，由队列来动态存储，由于是双进程，此时遍历出的路径就是一个回路，卡多来回的路径，因此只需要选出宝物总价值最大的路径即可，便可得出最终的结果。

给出代码

动态规划（DP）:可视化库graphics

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
#include<iostream>
#include<string.h>
#include<algorithm>
#include<graphics.h>
#include<stdio.h>

using namespace std;
const int maxn = 51;
#define mem(a,b) memset(a,b,sizeof(a))

int ma[maxn][maxn];
int dp[maxn][maxn][maxn][maxn];
int track[maxn][maxn][maxn][maxn][4];   //记录所走距离相同的点对的继承方式，动态规划的过程
int INDEX = 0; //全局变量,记录数值比较的结果 

int Max(int a,int b,int c,int d)
{
	int temp = 0;
	int m[4];
	m[0] = a;
	m[1] = b;
	m[2] = c;
	m[3] = d;
	for(int i=0;i<4;i++)
	{
		if(m[i]>temp)
		{
			temp = m[i];
			INDEX = i;
		}
	}
	return temp;
}

void Draw_track(int M,int N)
{
	int ta[maxn][maxn][2];
	for(int i=0;i<=M;i++)
	{
		int pos_x = (i-1)*45 + 12;
		for(int j=0;j<=N;j++)
		{
			int pos_y = (j-1)*45 + 12;
			ta[i][j][0] = pos_x;
			ta[i][j][1] = pos_y;
		}
	}
	setcolor(RGB(0,0,108));
	int x1=M-1,y1=N,x2=M,y2=N-1;
	line(ta[M][N][1],ta[M][N][0],ta[x1][y1][1],ta[x1][y1][0]);
	line(ta[M][N][1],ta[M][N][0],ta[x2][y2][1],ta[x2][y2][0]);
	while(dp[x1][y1][x2][y2])
	{
		if (x2==2&&y2==1)
			break; //此时画出了最后两个相同距离的点，可以在下面归于入口了
		line(ta[track[x1][y1][x2][y2][0]][track[x1][y1][x2][y2][1]][1],ta[track[x1][y1][x2][y2][0]][track[x1][y1][x2][y2][1]][0],ta[x1][y1][1],ta[x1][y1][0]);
		line(ta[track[x1][y1][x2][y2][2]][track[x1][y1][x2][y2][3]][1],ta[track[x1][y1][x2][y2][2]][track[x1][y1][x2][y2][3]][0],ta[x2][y2][1],ta[x2][y2][0]);
		int tem1 = track[x1][y1][x2][y2][0];
		int tem2 = track[x1][y1][x2][y2][1];
		int tem3 = track[x1][y1][x2][y2][2];
		int tem4 = track[x1][y1][x2][y2][3];
		x1 = tem1;
		y1 = tem2;
		x2 = tem3;
		y2 = tem4;
	}
	line(ta[1][1][1],ta[1][1][0],ta[1][2][1],ta[1][2][0]);
	line(ta[1][1][1],ta[1][1][0],ta[2][1][1],ta[2][1][0]);
}
int main()
{
	int times;
	cin >> times;
	while(times--)
	{
		//初始化局部最优解数组dp,值全为0
		mem(dp,0);
		//先输入卡多要走的地图数据
		int M,N,temp,i,j;
		cin >> M >> N;
		for(i=1;i<=M;i++)
			for(j=1;j<=N;j++)
			{
				cin >> ma[i][j];
			}		
		//填充局部最优解数组，遍历ma地图数组，模拟卡多分身为两个走到右下角，把所有可能的两个卡多同时所在的点遍历出来，并填充其值，当前带的宝物价值
		for(i=1;i<=M;i++)
		{
			for(j=1;j<=N;j++) //遍历到这里，找到第一个卡多所在位置(i,j)
			{
				//根据卡多1所在位置向下找到卡多2所在的位置（根据卡多1 2 所走的步数相同），注：不能再向上找了，因为就重复了
				for(int x=i+1;x<=M;x++)
				{
					int y = i+j-x;
					if(y<=0) //说明当前卡多1位置下，在卡多1所在的行之下，某行，不可能存在卡多2所在的位置,此时当前行及以下行对于填充dp数组无用
					{
						break;
					}
					dp[i][j][x][y] = Max(dp[i][j-1][x][y-1],dp[i][j-1][x-1][y],dp[i-1][j][x][y-1],dp[i-1][j][x-1][y]) + ma[i][j] + ma[x][y];
					switch(INDEX)
					{
					case 0: track[i][j][x][y][0] = i;track[i][j][x][y][1] = j-1;track[i][j][x][y][2] = x;track[i][j][x][y][3] = y-1;break;
					case 1: track[i][j][x][y][0] = i;track[i][j][x][y][1] = j-1;track[i][j][x][y][2] = x-1;track[i][j][x][y][3] = y;break;
					case 2: track[i][j][x][y][0] = i-1;track[i][j][x][y][1] = j;track[i][j][x][y][2] = x;track[i][j][x][y][3] = y-1;break;
					case 3: track[i][j][x][y][0] = i-1;track[i][j][x][y][1] = j;track[i][j][x][y][2] = x-1;track[i][j][x][y][3] = y;break;
					default:;
					}
				}
			}
		}
		//经过上面的遍历，局部最优解动态地规划，最终得到dp[M-1][N][M][N-1],接近正确答案。注：卡多1定过[M-1][N]，卡多2定过[M][N-1]；
		int result = dp[M-1][N][M][N-1] + ma[M][N];
		cout << "卡多最多能带出的宝物的价值是：" << result << endl;
		initgraph(1000, 800);	// 打开图形窗口
		setcolor(RGB(0,0,108));
		//line(10,10,100,100);
		IMAGE jpg;
		loadimage(&jpg,"Materier/2.jpg",1000,800);
		putimage(0,0,&jpg);
		setbkmode(TRANSPARENT);
		settextstyle(12,12,"宋体");
		settextcolor(RGB(40,30,80));
		char sz[5];//字符串
		for(i=1;i<=M;i++)
		{
			int pos_x = (i-1)*45;
			for(j=1;j<=N;j++)
			{
				int pos_y = (j-1)*45;
				sprintf(sz, "%d", ma[i][j]);//这句需要头文件#include <stdio.h>
				outtextxy(pos_y,pos_x,sz);
			}
		}
		Draw_track(M,N);
		outtextxy(10,(i-1)*45+25,"卡多最多可以带走宝物的价值是:");
		char resu[7];
		sprintf(resu, "%d", result);
		outtextxy(10,(i-1)*45+50,resu);
		getchar();
		getchar();
		closegraph();
	}
	return 0;
}

深度优先搜索（DFS）

OneRoad.h

1
2
3
4
5
6
7
8
9
10
11
12
13
#include<vector>

using namespace std;

class OneRoad
{
public:
	OneRoad();
	OneRoad(vector<vector<int> > tr,int su);
	void add_to_track(vector<int> m, int n);
	vector<vector<int> > track;
	int sum_value;
};

OneRoad.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include "OneRoad.h"

OneRoad::OneRoad()
{
	sum_value = 0;
}

OneRoad::OneRoad(vector<vector<int> > tr,int su)
{
	sum_value = su;
	track = tr;
}

void OneRoad::add_to_track(vector<int> m, int n)
{
	track.push_back(m);
	sum_value += n;
}

main.cpp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
#include<iostream>
#include<algorithm>
#include"OneRoad.h"

using namespace std;
#define maxn 51
int ma[maxn][maxn];
int M,N;
vector<OneRoad> V0;
vector<OneRoad> V1;

bool com(vector<int> a,vector<int> b)
{
	return a[2] > b[2];
}

void dfs(int tag,int a,int b,int index)//tag为0代表找第一条路，tag为1代表找第二条路
{
	vector<int> mm;
	mm.push_back(a);
	mm.push_back(b);
	if(tag==0)//第一条路
	{
		V0[index].add_to_track(mm,ma[a][b]);
		bool tag_right = false;
		bool tag_down = false;
		int num = 0;
		if(a<M-2)
		{
			tag_down = true;
			num ++;
		}
		if(b<N-1)
		{
			tag_right = true;
			num ++;
		}
		if(num==1)
		{
			if(tag_down)
				dfs(0,a+1,b,index);
			else
				dfs(0,a,b+1,index);
		}
		else if(num==2)
		{
			V0.push_back(OneRoad(V0[index].track,V0[index].sum_value));//把新创建的对象放入全局对象数组
			dfs(0,a,b+1,V0.size()-1); //必须马上执行这个语句,后执行下面的语句，保证index
			dfs(0,a+1,b,index);       // ...........
		}
	}
	else  //第二条路
	{
		V1[index].add_to_track(mm,ma[a][b]);
		bool tag_right = false;
		bool tag_down = false;
		int num = 0;
		if(a<M-1)
		{
			tag_down = true;
			num ++;
		}
		if(b<N-2)
		{
			tag_right = true;
			num ++;
		}
		if(num==1)
		{
			if(tag_down)
				dfs(1,a+1,b,index);
			else
				dfs(1,a,b+1,index);
		}
		else if(num==2)
		{
			V1.push_back(OneRoad(V1[index].track,V1[index].sum_value));//把新创建的对象放入全局对象数组
			dfs(1,a,b+1,V1.size()-1);  //必须马上执行这个语句,后执行下面的语句，保证index
			dfs(1,a+1,b,index);        //  ......
		}
	}
}

bool is_contra(OneRoad a,OneRoad b)
{
	bool same = false;
	for(int i = 0;i<M+N-3;i++)  //最终的路径的结点数均应该为M+N-3
	{
		if(a.track[i][0] == b.track[i][0] && a.track[i][1] == b.track[i][1])
		{
			same = true;
			break;
		}
	}
	return same;
}

int main()
{
	int i,j;
	int times;
	cin >> times;
	while(times--)
	{
		cin >> M >> N;
		for(i=0;i<M;i++)
			for(j=0;j<N;j++)
			{
				cin >> ma[i][j];
			}
		OneRoad init0;
		OneRoad init1;
		V0.clear(); //清除原有的
		V1.clear(); //清除原有的
		V0.push_back(init0);
		V1.push_back(init1);
		dfs(0,0,1,0);  //第一条路径的深度优先遍历
		dfs(1,1,0,0);  //第二条路径的深度优先遍历
	
		//把路径的所有组合遍历出
		vector<vector<int> > comp;
		for(i = 0;i<V0.size();i++)
		{
			for(j = 0;j<V1.size();j++)
			{
				vector<int> temp;
				temp.push_back(i); //代表V0中的某个对象的坐标
				temp.push_back(j); //......
				temp.push_back(V0[i].sum_value+V1[j].sum_value); //权值价值和
				comp.push_back(temp);
			}
		}
		sort(comp.begin(),comp.end(),com); //按价值排序组合
		//接下来选V0,V1容器中不冲突的最大价值的两个路径对象组成一个回路即可
		int ind;
		for(i = 0;i<comp.size();i++)
		{
			if(!is_contra(V0[comp[i][0]],V1[comp[i][1]]))
			{
				ind = i;
				break;  //这个语句一定会执行
			}	
		}
		cout << "卡多最多能带出宝物的价值是：" << comp[ind][2] + ma[M-1][N-1] << endl;
		cout << "路径:" << endl;
		cout << "(" << 0 << "," << 0 << ")" << " ";
		for (i = 0;i<V0[comp[ind][0]].track.size();i++)
		{
			cout << "(" << V0[comp[ind][0]].track[i][0] << "," << V0[comp[ind][0]].track[i][1] << ")" << " ";
		}
		cout << "(" << M-1 << "," << N-1 << ")" << " ";
		for (i=V1[comp[ind][1]].track.size()-1;i >= 0;i--) //倒序输出
		{
			cout << "(" << V1[comp[ind][1]].track[i][0] << "," << V1[comp[ind][1]].track[i][1] << ")" << " ";
		}
		cout << "(" << 0 << "," << 0 << ")" << " ";
		cout << endl;
	}
	return 0;
}

广度优先搜索(BFS)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;
#define maxn 51
int ma[maxn][maxn];

bool cmp(vector<int> m,vector<int> n)
{
	return m[4]<n[4];
}

int main()
{
	int times;
	cin >> times;
	while(times--)
	{
		int M,N;
		cin >> M >> N;
		for(int i=0;i<M;i++)
			for(int j=0;j<N;j++)
			{
				cin >> ma[i][j];
			}
		vector<vector<int> > V;
		int prim = -1; //一个结果的指针，index为prim之前的V内的数据被忽略
		int step = 0;
		step += 1;  //开始走一步
		prim += 1;  //表示一步之后结果的起始位置
		vector<int> head;
		head.push_back(0);
		head.push_back(1);
		head.push_back(1);
		head.push_back(0);
		head.push_back(ma[0][1]+ma[1][0]);
		V.push_back(head);
	    
		while(++step<=M+N-3)
		{
			int size = V.size();  //重新获取大小
			for(int i = prim ;i<size;i++)
			{
				if(V[i][0]+1<M && V[i][2]+1<M)
				{
					vector <int> temp;
					temp.push_back(V[i][0]+1);
					temp.push_back(V[i][1]);
					temp.push_back(V[i][2]+1);
					temp.push_back(V[i][3]);
					temp.push_back(ma[V[i][0]+1][V[i][1]]+ma[V[i][2]+1][V[i][3]] + V[i][4]);
					V.push_back(temp);
				}
				if(V[i][1]+1<N && V[i][2]+1<M)
				{
					vector <int> temp;
					temp.push_back(V[i][0]);
					temp.push_back(V[i][1]+1);
					temp.push_back(V[i][2]+1);
					temp.push_back(V[i][3]);
					temp.push_back(ma[V[i][0]][V[i][1]+1]+ma[V[i][2]+1][V[i][3]] + V[i][4]);
					V.push_back(temp);
				}
				if(V[i][0]+1<M && V[i][3]+1<N && !(V[i][2]-V[i][0]==1 && V[i][1]-V[i][3]==1))
				{
					vector <int> temp;
					temp.push_back(V[i][0]+1);
					temp.push_back(V[i][1]);
					temp.push_back(V[i][2]);
					temp.push_back(V[i][3]+1);
					temp.push_back(ma[V[i][0]+1][V[i][1]]+ma[V[i][2]][V[i][3]+1] + V[i][4]);
					V.push_back(temp);
				}
				if(V[i][1]+1<N && V[i][3]+1<N)
				{
					vector <int> temp;
					temp.push_back(V[i][0]);
					temp.push_back(V[i][1]+1);
					temp.push_back(V[i][2]);
					temp.push_back(V[i][3]+1);
					temp.push_back(ma[V[i][0]][V[i][1]+1]+ma[V[i][2]][V[i][3]+1] + V[i][4]);
					V.push_back(temp);
				}
				prim += 1; //相当于队列最前面的元素出队
			}
		}
		sort(V.begin()+prim,V.end(),cmp);
		int result = V[V.size()-1][4] + ma[M-1][N-1];
		cout << "卡多能带走宝物的最大总价值是:" << result << endl;
	}
	return 0;
}

请评论

所有代码已经细致地进行过调试，请放心使用，思路和功能确保正确，但实现的手段略显拙劣，请提出你改进的建议，感激不尽。

算法
#编程
探寻宝藏_动态规划和路径遍历
https://blog.wangxk.cc/2019/06/24/探寻宝藏-动态规划和路径遍历/
作者
Mike
发布于
2019年6月24日
许可协议