环状链表相关

环状链表的检测

环状链表的检测比较好办,使用双指针的方法

一个快指针，一个慢指针。快指针步进值是2，慢指针的步进值是1

无环的时候：快指针走的快，慢指针走的慢，因为是直线型的，快指针先到达链表结尾便停止了，所以快慢指针永远不会相遇。

有环的时候：慢指针没走到环上的时候，因为是直线，所以不会相遇。但是慢指针一旦到达入环点，就可以看做慢指针在快指针的前面，他们之间是一定有距离的（0也算是距离,distance>=0），因为快指针比慢指针快，所以他们一定会相遇。

力扣-环形链表

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode n1 = head; // 慢结点
        ListNode n2 = head; // 快结点
        while(n2 != null){
            n1 = n1.next;
            try{
                n2 = n2.next.next;
            }catch(NullPointerException e){
                return false;
            }
            if(n1 == n2){
                return true;
            }
        }
        return false;
    }
}

注意：步进值设置为1和2是很有讲究的

1. 每次不用跨步太大，节省性能

2. 可以达到两指针的距离每次减一的平稳下降，例如如果距离是8，那么距离序列就是[8,7,6,5,4,3,2,1,0]，0即为相遇。举个反例，环长度 为9，快指针距离慢指针为5, 快指针速度为4，慢指针速度为1, 那么距离序列即为[5,2,-1(8),5,2,-1(8),5,2,-1(8),5,2,-1(8),5,2,-1(8),5,2,-1(8),5,2,-1(8),……] ，这样即便是有环也永远不会相遇了。

   不是跑步模型，是跳一跳的模型，只有落下时判断是否相遇程序才能处理【不管在空中的x轴上是否相遇】。

环状链表的入环点

面试题 02.08. 环路检测

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode n1 = head; // 慢结点
        ListNode n2 = head; // 快结点
        while(n2 != null){
            n1 = n1.next;
            try{
                n2 = n2.next.next;
            }catch(NullPointerException e){
                return null;
            }
            if(n1 == n2){
                break;
            }
        }
        if(n2 == null){
            return null;
        }
        // 走到这里就是一定有环了
        n1 = head;
        while(n1!=n2){
            n1 = n1.next;
            n2 = n2.next;
        }
        return n2;
    }
}

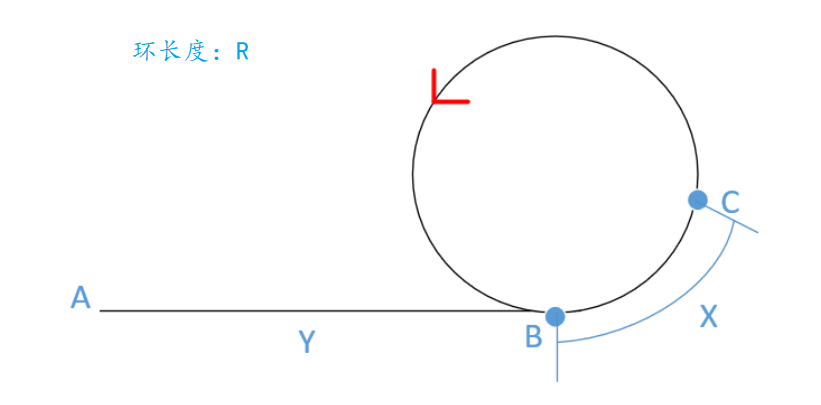
可以推导出：

2（X+Y）= Y+NR+X

消去两边 即是：X+Y = NR

NR-X = Y : 所以，快指针从快慢指针相遇点开始出发，步进为1，降为慢指针。慢指针从头结点出发，最终一定会相遇于入环点。

便于理解： 我们一定可以推导出：0<X<=R (X是相遇前慢指针在环上走的距离)，N>=1,Y可以等于0，X一定不为0

环状链表的环长度

这个就十分简单了，既然是环，快慢指针就一定有相遇点

找环上任意一点记录，再次经过该点时走过的距离即是环的长度，

相遇点一定是在环上，所以选相遇点使用。